One of the nicest properties of quantum computing circuits is the fact that you can achieve the same goal
with a fewer number of steps compared to classical computer, and it has been a lot of fun for me to discover
how to implement such algorithms.
I wanted to write about an algorithm I spent some time thinking about and wrestling with. This particular quantum
circuit does not provide an improvement over a classical one (there are algorithms tacking similar problems that ac
tually do provide speed-ups), but it was really nice to see how to solve a problem using quantum thinking as opposed to
classical thinking.
The problem consist of coming up with an algorithm to learn the bits of a hidden string s. For this problem we restrict
the string s to be a string of 0 and 1, e.g.: 100110
The classical algorithm is quite simple. It can be summarized as follows: test every bit of the string with the and operation and a 1, if the result is
1 then the bit is a 1 otherwise the bit is a 0.
To solve this problem using quantum computing I decided to break the algorithm into two parts. The first part will encode
a unitary function whose main purpouse is some information from any secret string. The second part of the
algorithm consists in preparing a state that represents all the possible states of a binary string s of size n.
The first part of the algorith is called an oracle.
The oracle
As mentioned before, the first part of the problems boils down to finding a quantum circuit that can be used to extract
information from any string s. By doing some exploration and due to previous experinece I had on similar problems
I settled on the oracle that is would basically calculate the sum mod 2 of $x_i$ * $s_i$ where $x_i$ is the ith bit of
an arbitrary string x and $s_i$ is the ith bit of the hidden string s. Or in other words:
$$ (\sum_{i=0}^{n}s_i * x_i)\ mod\ 2 $$
The above is equivalent to calculating the parity of s when x equals to 111...1.
Next, then is the problem of coming up with an algorithm that encodes the above unitary, here I did testing of
different circuits looking for patterns, starting with smaller strings allowed me to find patters in the circuits. For
example the circuit for the string 101 looks like this:
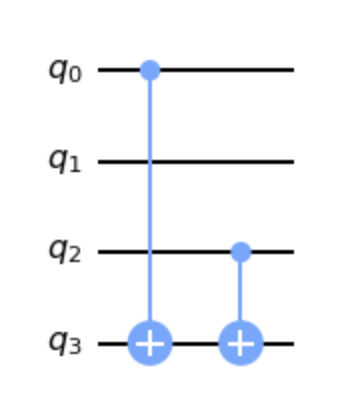
The pattern I found was basically CNOTing all the 1 bits of the secret string. Thus, I coded up a function whose input
is an arbitrary string s and the output is a quantum circuit that encodes the above unitary for the input string s.
The width of the circuit varies grows linearly with the length of s(which is not great), and the number of gates grows
linearly with the number of 1 in s, they are all CNOT gates which is implemented in most quantum hardware. Further
there are no operations between the input qubits, only between the inputs and output qubit.

The search circuit
The world of quantum computing revolves around designing a circuit that creates an interesting superposition state, that
can later be exploited to process a particular computation. One common technique to do is to create the super position
where all possible states in a quantum register have equal measuring probability, this state is called the uniform
superposition. For example in a 2 qubit register the uniform super position would be the state:
$$ \psi = \frac{1}{4}(|00> + |01> + |10> + |11>) $$
More generally the uniform super position of an n-qubit register is:
$$ \psi = \frac{1}{\sqrt{2^n}}\sum_{0}^{2^n-1}|x> $$
Such a circuit can be created via hadamard gates applied to each of the input qubits for a quantum register set to 0
The final circuit
By combining both parts we get the final circuit.
At the end of the circuit we apply hadamards to finalize the search circuit and read the measurement to classical bits.
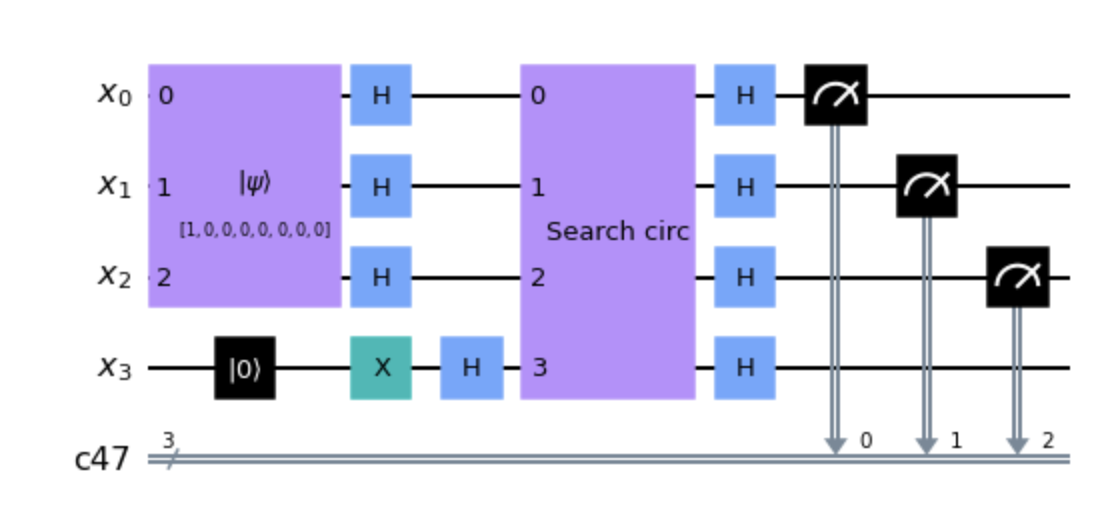
The circuit is initialized with the state |0> plus an ancilla qubit set to |1> which helps us encode the oracle unitary
and the uniform superposition. Notice the circuit labelled search circ is actually built for the hidden string s and
it varies depending on s.
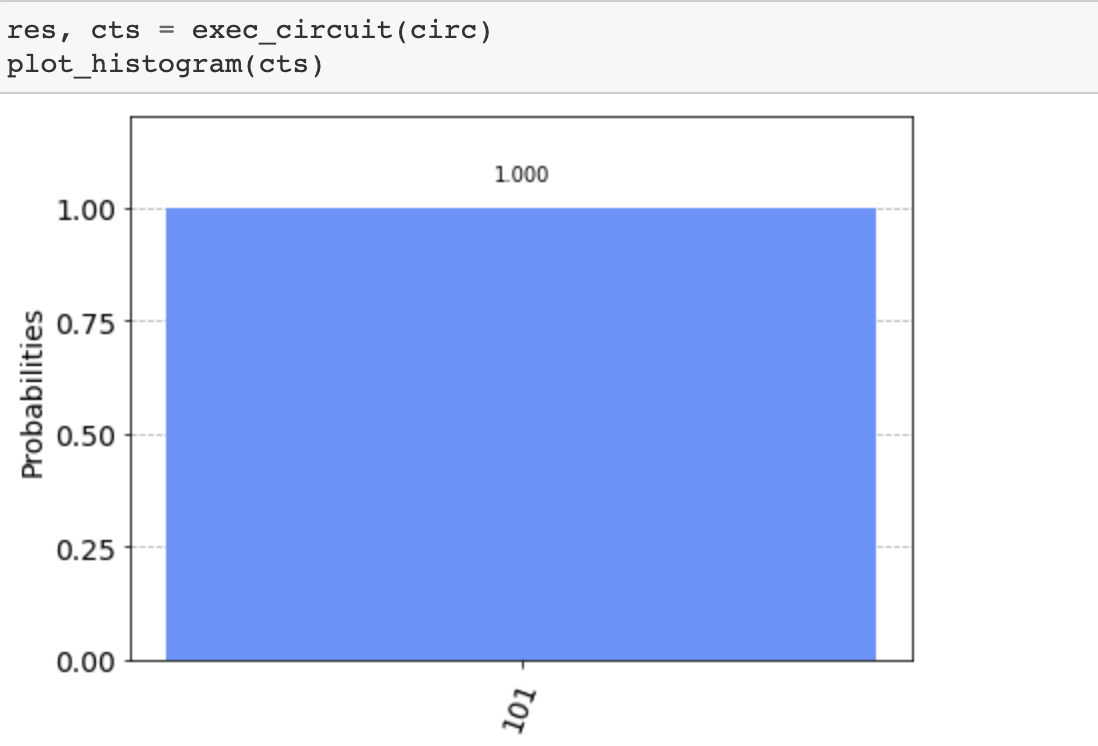
Finally when running the circuit we should expect to read back the hidden string s in the classical bits. Interestingly
we only need to run this circuit one time to properly discover the string s. Recall the classical algorithm needs
to iterate through each of the bits in the string s in order to discover s.
For the complete code, feel free to look at this repository
which contains a runnable notebook you can play with.